Todos esses triângulos são formados por coeficientes binomiais (números binomiais), a sua organização é feita da seguinte forma:
• Todos os coeficientes de mesmo numerador são colocados na mesma linha.
• Todos os coeficientes de mesmo denominador são colocados na mesma coluna.
Veja como ficaria a construção do triângulo de Pascal:
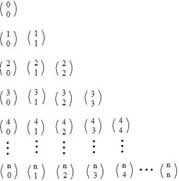
Cada coeficiente binomial que forma o Triângulo de Pascal possui um valor numérico encontrado através: dos casos particulares dos coeficientes, das suas propriedades ou da fórmula da combinação. Veja como ficaria o Triângulo de Pascal com seus valores numéricos:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1 . . .
. . . . .
. . . . .
. . . . .
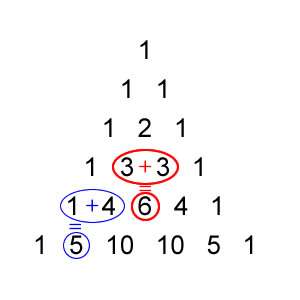
Uma das formas (a mais usual) de construir um triângulo de Pascal é na forma de um triângulo isósceles, preenchemos com 1´s os lados do triângulo a partir do vértice superior e para obter os números em cada linha, somamos os dois números logo acima dele na linha superior, por exemplo: 2=1+1, ou seja, o número 2 da terceira linha é igual à soma de 1+1, os dois números logo acima dele na segunda linha, assim 3=1+2, 6=3+3, 10=4+6,etc. A figura abaixo mostra o triângulo de Pascal até a sexta linha:
As propriedades interessantes do triâgulo de Pascal são as seguintes:
Cada linha representa os números binomiais na expansão de (x+y)n, n≥0. Por exemplo,
(x+y)3=1.x3 + 3x2y + 3xy2 + 1.y3 e na quarta linha temos 1 3 3 1.
Ocorre que sabemos pelo Binômio de Newton que cada número do triângulo de Pascal será um coeficiente binomial, ou seja, na (n+1)-ésima linha o (k+1)-ésimo número será:
Por exemplo, na 5ª linha o terceiro número é:
Pela construção do triângulo de Pascal, temos:
Relação de Stiffel
Por exemplo, 10=4+6, ou seja:
A soma de todos os números na (n+1)-ésima linha é igual a 2n. Por exemplo, na 1ª linha a soma é 20=1, na 4ª linha 23=8, etc.
O triângulo de Pascal é simétrico em relação a sua altura pois
Se somarmos a diagonal também temos o seguinte resultado:
Por exemplo, na 3ª diagonal: 1+3+6+10=20, ou
Nenhum comentário:
Postar um comentário